Коло і трикутник

Коло, описане навколо трикутника

Коло називають описаним навколо трикутника, якщо воно проходить через усі вершини трикутника. Трикутник при цьому має назву вписаного.

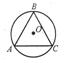
Теорема.   Навколо кожного  трикутника можна описати лише одне коло. Його центром є точка

                перетину серединних перпендикулярів двох сторін трикутника.

Наслідок. Серединні перпендикуляри усіх трьох сторін довільного трикутника проходять через

                одну й ту саму точку.

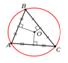
Наслідок.     Через будь-які три точки, які не лежать на одній прямій, можна провести коло,

                                 і лише одне.

Центр кола, описаного навколо трикутника, може лежати у внутрішній або зовнішній області даного трикутника або на його стороні.

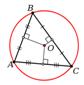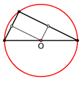
Теорема. Центром кола, описаного навколо прямокутного трикутника,

              є середина його гіпотенузи.

Теорема. З будь-якої точки кола його діаметр, що не виходить з цієї точки, видно

               під прямим кутом.

Наслідок.  Діаметр кола, описаного навколо прямокутного трикутника, дорівнює його

                  гіпотенузі.                                                                                                                                                    

Коло, вписане в трикутник

          Коло називається вписаним у трикутник, якщо воно дотикається до всіх сторін трикутника. Сторони трикутника є дотичними до вписаного в нього кола. Трикутник при цьому називається описаним навколо кола.

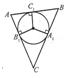
Теорема.  У кожний  трикутник можна вписати коло і лише одне. Його центром є

                 точка перетину двох бісектрис трикутника.

Наслідок.   У кожному трикутнику, всі три бісектриси перетинаються в одній точці

Презентація

Практична робота.

Накресліть довільний трикутник  і опишіть навколо нього коло (впишіть у нього коло).

Задача.     Дано діаметр АВ і хорду ВС. Знайдіть внутрішні кути трикутника АВС, якщо кут АОС                       

                  дорівнює 130˚.

Розв’язання:

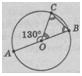
Трикутник ВОС рівнобедрений, оскільки ОВ = ОС як радіуси кола. Отже, кути В і С при основі цього трикутника рівні.

За властивістю зовнішнього кута трикутника  < В + < С = 130˚. Тоді < В = <С =130˚: 2 = 65˚.

Кути АОС і ВОС суміжні, тому < АОС + < ВОС = 180˚, звідки < ВОС = 180˚ - 130˚ = 50˚.

Відповідь. 65˚, 65˚, 50˚.

Задачі.

1. Кут В прямокутного ∆ АВС дорівнює 60˚, катет ВС = 5 см. Знайдіть радіус описаного кола.
2. Точка дотику кола, вписаного у трикутник, ділить одну із сторін на відрізки 5 см і 7 см. Знайдіть сторони трикутника, якщо його периметр 44 см.

Тест.